Etude XVIII is one of the densest and most difficult of all the Freeman Etudes. In section 1.2.1 I examine one possible methodology of learning how to deal with the extreme technical challenges at hand, through which I can incorporate as much detail as possible while creating a state of readiness to react to the unexpected that will appear in the moment of performance. Section 1.2.1 thus addresses questions of practice/advance preparation, and presents examples relating to decisions made in the moment of performance.

The basic recognition of pitches in Freeman Etudes does not in itself present a specifically challenging issue. As soon as the score is examined more closely, however, the challenging aspects and exceptions to a “standard” reading of otherwise standard-looking notation come to the fore.

The first of these exceptions involves inflectional markings added to the standard notational symbols for pitch (figure 1.2.1.1).

Figure 1.2.1.1: Pitch inflections - top: symbols for pitch inflections; bottom: example of pitch inflection

While the tones are ‘conventionally pitched or indeterminately microtonally sharp or flat’,^[1] additional symbols for slight changes, as seen in the top part of figure 1.2.1.1, include:

• - starting from the pitch and going slightly up
• - going into the pitch from slightly above the pitch
• - going into the pitch from slightly under
• - starting from the pitch and going slightly under
• - starting from the pitch going slightly above and returning to the original pitch
• - starting from the pitch going slightly under and returning to the original pitch
• - starting from the pitch going slightly above and then under
• - going from slightly under to slightly above and arriving to the pitch
• - starting from the pitch then going slightly under and then slightly above
• - going from slightly above, then going slightly under and then arriving to the pitch
• - starting from the pitch, going slightly above, then going slightly under, and then arriving back to the pitch
• - starting from the pitch, going slightly under, then going slightly above, and ending back on the pitch.

Another unconventional addition is the way that Cage depicts the timing of events. The division and placement of events in time – metre and rhythm – are represented by two horizontal lines underneath each system (figure 1.2.1.2).

Figure 1.2.1.2: Representation of time

The lower line denotes “bar lines”: this lower timeline is divided into seven equal segments, which, as Cage writes in the preface to the published score of Books 1 and 2, could be considered equivalent to ‘measures’ (in inverted commas in the original). Each of these segments indicates the passing of an equal amount of time. The goal is not only to maintain the established time-length per measure from system to system of one Etude but to be consistent with this time-length throughout all the Etudes. Cage additionally instructs that the time-length per ‘measure’ ‘should be short rather than long, as short a time-length as [the performer’s] virtuosity permits (circa 3 seconds)’.^[2] This instruction, the minimum ideal of 3 seconds, becomes one of the elements crucial to the “impossibility” of the Etudes in performance. But also, through Arditti, the alternative perception and interpretation of this instruction is what ultimately opens the path to finding solutions to said impossibilities.

The upper line represents each individual sound event in space-time. These moments are depicted with the use of the same short vertical lines as the ‘measure’ divisions in the lower line, but their function differs. In Books 1 and 2, Cage calls these ‘ictae’, and in Books 3 and 4 ‘ictuses’. The lengths of these ictae/ictuses act as determinants of rhythm. But unlike conventionally western classical notation of note lengths and rhythm, ictae/ictuses do not give the same immediate clarity of duration.

There are three ways in which a performer can approach interpreting these durations and rhythms. One way is by intuitively assessing approximate lengths between ictuses, and their relationship within the ‘three-second measure’ segments. But due to the density of ictuses, or in other places their sparsity, in addition to all other information that a performer has to deal with in the moment, this would result in very loosely defined happenings within the space-time.

The second possibility is to precisely measure the space between each ictus. Although this is a time-consuming task, especially when done for each of the 32 etudes, this approach produces reliable durations for each pitch.

Following is the example of one such calculation (figure 1.2.1.4), for the first measure (figure 1.2.1.3).

Figure 1.2.1.3: First measure from Etude XVIII

• - Starting point: there is 30.51mm (3.05cm) per ‘measure’ (in the Edition Peters published score)
• - 30.5mm = 3 seconds (or 3000ms)
• - the first measure contains 13 ictuses

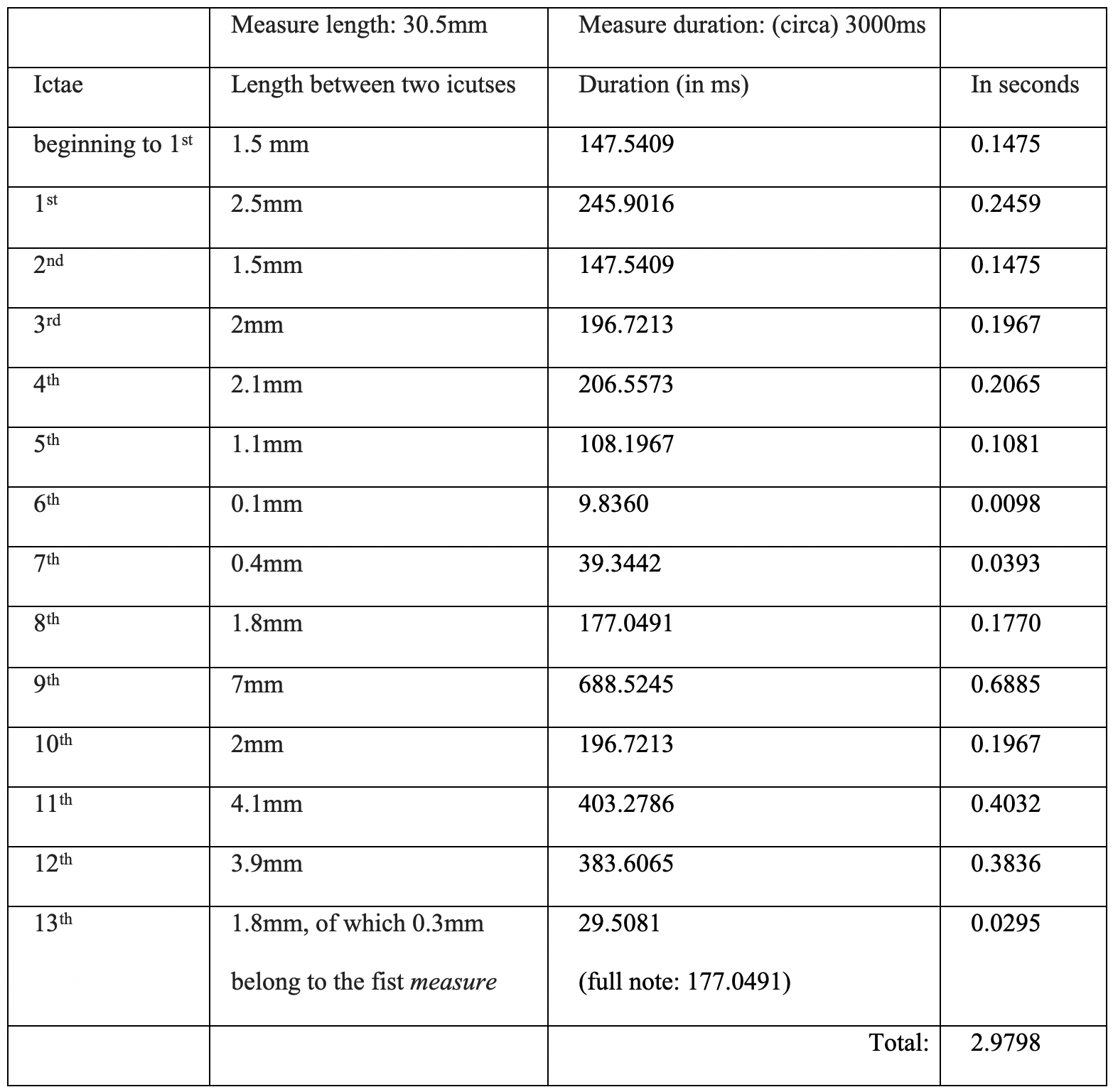
Figure 1.2.1.4: Calculation transferring distances to time duration of each of the sound events in the first measure of Freeman Etude XVIII

Using this calculation, it would be possible to go even further in this approach and “re-notate” the rhythm with the use of notation that is more accessible to the eye (figure 1.2.1.5).

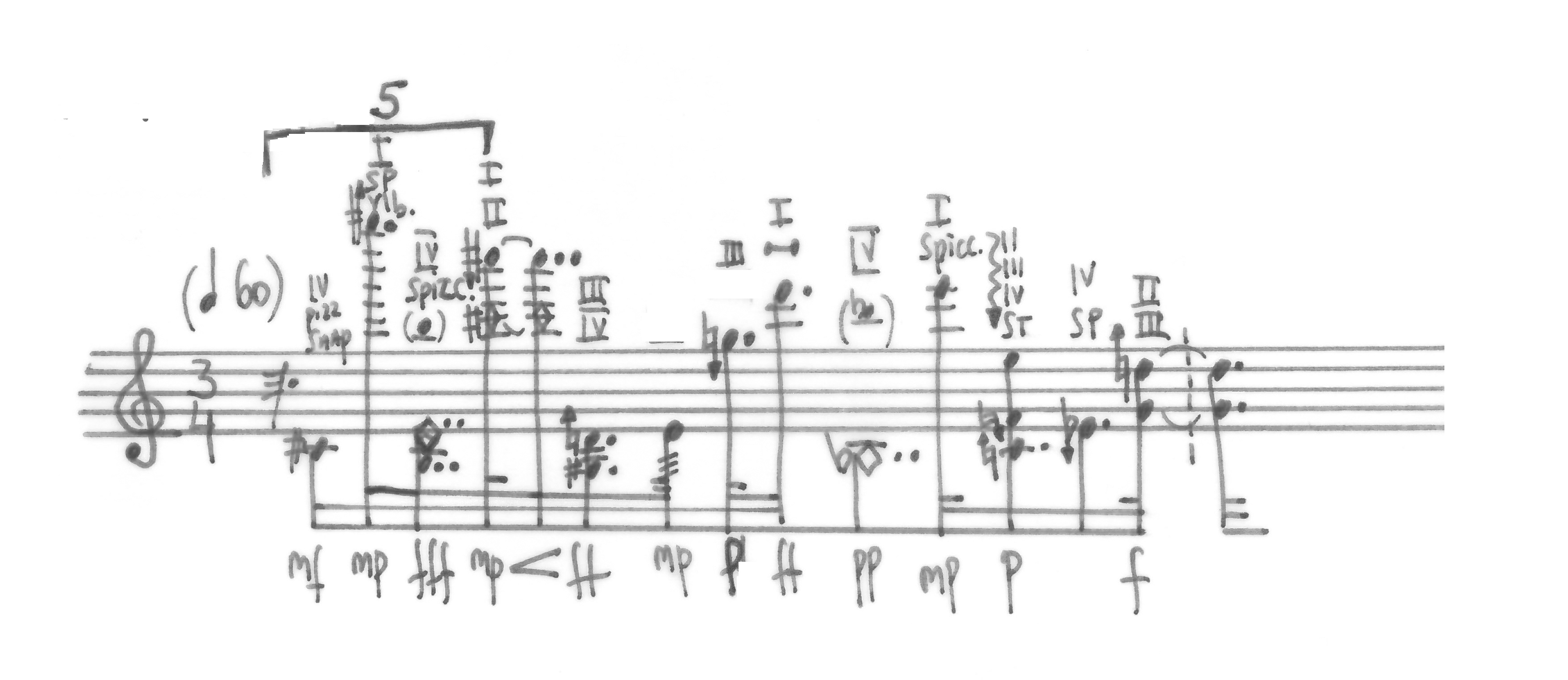
Figure 1.2.1.5: First measure of Etude XVIII, my “re-notation” with standard approach to rhythmic notation

The ‘measure’ of ‘circa 3 seconds’ was assigned a 3/4 time signature, with a tempo of quarter note = 60. With this organisation of space-time, and with 1 second per quarter note as a premise, ictuses 0–4 were (roughly) assigned to the first quarter note, ictuses 5–9 to the second and ictuses 10–13 to the third.

Although this approach can be considered useful for grasping some of the more complex time-space divisions in the beginning phases of work, through this new visual representation of the material the focus of the score would shift largely to rhythm. This visually imposed shift is bound to destroy both the musical continuity and performative energy that Cage’s notation conveys to the performer.

The third approach, and the one that I personally have settled on, is a combination of the two previously outlined. For me, the use of the original score layout of the Etudes in performance is imperative, but so is the work of calculating time division in the first phases of preparation. Although precise calculation (or re-notation) does not guarantee an “accurate” sounding of rhythm in portions with dense ictuses, knowing the duration of longer ictuses is of great importance for the final form and for constructing an interpretation. Performative indeterminacy is certainly present in the moment of performance (because of all the previously described elements at play), but the identification of longer durations can provide anchor points among other, faster-changing ictuses and thus keep the general form and pace in place. The challenge of the division of time and the placement of events increases further when it comes to Etude XVIII, due to the appearance of additional note ‘segments’ – as will now be discussed in section 1.2.2.

• ^[1]John Cage, Freeman Etudes Books 3&4, performance notes, Edition Peters No. 66831cd (London: Peters Edition, 1992), p.1.
• ^[2]Cage, Freeman Etudes, p.1.

BACK to WORKSPACE